This paper published in January 2023 in Nature describes the unexpected consequences of geological strain rates on the mechanical behavior of bridgmanite-periclase aggregates

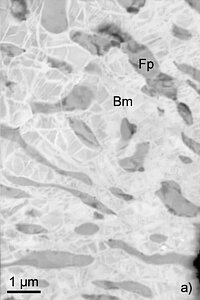
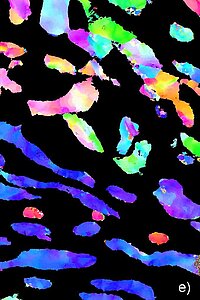
The lower Earth's mantle (which extends from 670 km depth to the planet's core) is mainly composed of two solid phases, a magnesium silicate, bridgmanite, the majority phase (ca. 80 %), associated with a magnesium oxide, periclase. These minerals, subjected to extreme conditions (pressures ranging from 25 to 135 GPa, temperatures between 2000 and 2800 K) deform slowly over geological time scales to produce mantle convection. The mechanical behavior of these two phases thus plays a major role in the dynamics of the Earth. In recent years, mechanical deformation tests of small assemblies of bridgmanite and periclase, carried out in the laboratory (e.g. Girard et al. 2016), have shown that periclase is much softer than bridgmanite. The figure below presents the microstructure resulting from one of their deformation experiments performed at 27 GPa, 2130 K and 3x10^-5 s^-1. One can see very elongated and deformed grains of ferropericlase which has taken most of the strain (Figures from Nzogang et al. 2018, Left: virtual Bright Field; Right: inverse pole figure map of ferropericlase corresponding to the compression direction (vertical))

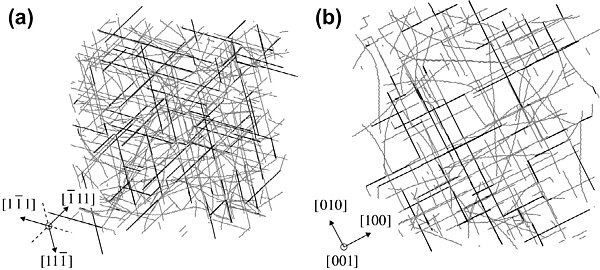
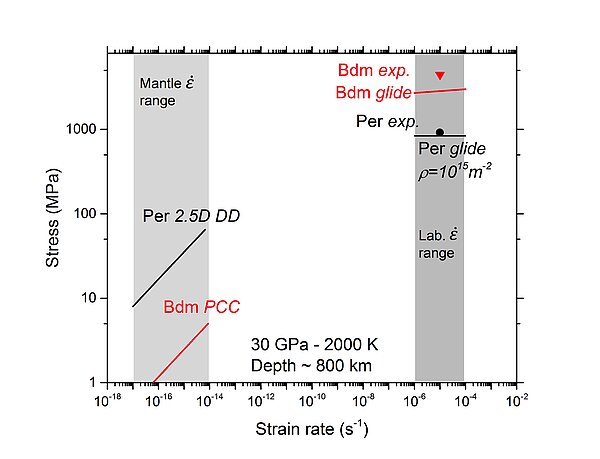
This paper is based on our multiscale numerical modeling approach initiated in the RheoMan project, with a focus on creep under high pressure. MgO has been the subject of a particularly strong modeling effort in our team (Amodeo et al. 2018). We have modelled dislocation cores structures and predicted a change of slip systems from 1/2<110>{110} at low pressure to 1/2<110{100} at high pressure (Carrez et al. 2009a). Based on a kink-pair model, we have described the thermal activation of dislocation glide, first at ambient pressure with a good agreement with experimental results (Carrez et al. 2009b, Amodeo et al. 2011) and then at high pressure (Amodeo et al. 2012). This multiscale modeling approach has made it possible for the first time to take into account simultaneously the effects of pressure, temperature AND strain rate in the description of plasticity by dislocation glide (Cordier et al. 2012). MgO has many slip systems which potentially leads to many interactions (Carrez et al. 2005). These interactions may form junctions which are energetically stable and are expected to promote strong forest strengthening at high temperature. We have described this behavior with large scale dislocation dynamics simulations (Amodeo et al. 2014, see figure below). Using this model, we have been able to model the behavior of ferropericlase reported in Girard et al. (2016). This apprears in Figure 3 of our paper (Per glide).

In the mantle, at high temperature and under very low stresses, MgO deforms by creep which involves a combination of dislcoation glide and climb. This behavoir has been modelled by Reali et al. (2017) by 2.5D dislocation dynamics providing a proof of feasibility by comparison with ambient pressure creep data.

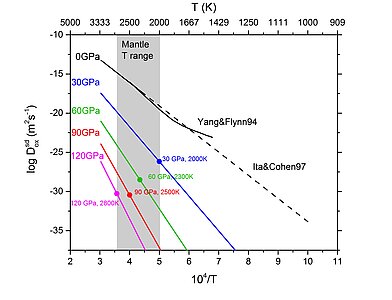
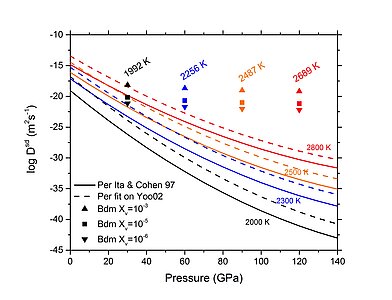
In this paper, we apply this creep model to the pressure and temperature conditions of the lower mantle. To do so, we need to know the ionic diffusion data that ultimately control the deformation. In MgO, the slowest diffusion is that of oxygen. We have based our model on the data of Ita and Cohen (1997) which allow to take into account simultaneously the effects of pressure and temperature. These data produces values of diffusion coefficients that are in agreement with the most reliable experimental results on intrinsic O diffusion from Yang and Flynn (1994). We thus obtain diffusion data for five (P,T) couples that correspond to different depths along the geotherm in the lower mantle.

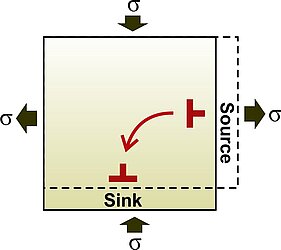
Our modeling leads to a behavior that can be described classically by a power law with a stress exponent n=3.1. This behavior however becomes remarkable when compared with the creep data of the other phase: bridgmanite. We also worked a lot on the modeling of this silicate so important for the rheology of the lower mantle. We started by modeling the core structure of the dislocations (Hirel et al. 2014), which is essential data to evaluate the lattice friction they are subjected to. This lattice friction is very important, and it increases very strongly under the influence of pressure in the range that corresponds to the lower mantle (Hirel et al. 2014). Modeling of thermal activation of slip by the kink-pair mechanism was performed by Kraych et al. (2016a). Even at high temperatures, lattice friction remains significant. This model is able to account very well for the high stresses observed in the experiments of Girard et al. (2016) as shown in Figure 3 of the paper (Bdm glide). It is also able to account for the influence of strain rate without extrapolation. The results of Kraych et al. (2016b) show that at mantle strain rates the lattice friction is lower, but still far too large to allow dislocations to glide in bridgmanite under natural conditions. It was therefore necessary to imagine another mechanism to account for the deformation of bridgmanite under natural conditions. In 2015, based on the work of Nabarro (1967), we proposed a pure dislocation climb creep mechanism (Boioli et al. 2017). In this mechanism, deformation is produced by the pure climb of edge dislocation loops that exchange vacancies. This mechanism can be seen as an extension of the Nabarro and Herring diffusion creep mechanism with dislocations (not grain boundaries) acting as sources and sinks of vacancies. It has the advantage of providing a characteristic distance of diffusion (the distance between dislocations) much more flexible than the grain size.

Taking this pure climb creep model applied to bridgmanite, Reali et al. (2019) showed that it was possible to account for viscosity values perfectly consistent with those estimated in the lower mantle. If we take these values for bridgmanite, and compare them to those obtained in this study for MgO, we are surprised to find that bridgmanite deforms more easily under low stress than MgO.

Indeed, in bridgmanite, the diffusion is controlled by the cations whose mobility is less affected by the pressure than the oxygen ion in the very compact structure of MgO.

This study demonstrates that knowledge of rheology in the extreme conditions of the Earth's mantle cannot emerge from the simple extrapolation of experimental data. The very low strain rates (and therefore very low stresses) of mantle convection require the activation of adapted mechanisms that are not necessarily the same as those activated in the laboratory. In this case, in these high pressure phases (such as bridgmanite) diffusion is too slow to produce finite deformations in experiments. The only solution is then to increase (strongly) the stress until dislocation glide is activated. In the mantle the stress is too low and it is the time that allows, slowly, the vacancies to diffuse and thus promote the climb of dislocations.

At the end of this work, a new vision of the lower mantle emerges. Bridgmanite dominates everything. Being the majority phase, its rheology is that of the aggregate. The low volume fraction of periclase does not allow it to play a significant role. This type of behavior can make one think of boudinage in the rock record (see image below of brecciated dolostone rocks of the Panamint Range (Wildrose Area, Death Valley National Park), courtesy J.M. Jackson), where boudins develop in a rigid, ‘stronger,' rock layer among less competent, ‘weaker,' rock.

An other analogy is provided by chunky peanut butter. We had thought for decades that periclase was the ‘oil' in peanut butter, and acted as the lubricant between the harder grains of bridgmanite. This view has led to much speculation about the possible dispersal state of the periclase in the aggregate forming, or not, an interconnected phase. Based on this new study, this question is no more relevant. It turns out that periclase grains act as the ‘nuts' in chunky peanut butter. Periclase grains just go with the flow and don't affect the viscous behavior.