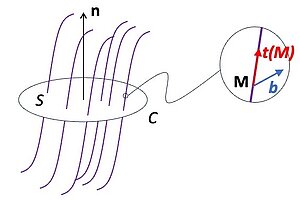
Nye has introduced a tensor α (so-called Nye's tensor) to calculate the net Burgers vector of the dislocation line, or of the set of dislocation lines crossing the surface S, assuming it is non-zero.

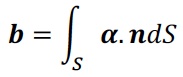
The Nye tensor can therefore be used to determine so-called geometrically necessary dislocations which are needed to accommodate for plastic strain gradients in a deformed material.

The Nye tensor is a second rank tensor which writes:

Where b is the Burgers vector of the dislocation line element of unit vector t

In terms of components, one writes:

α_ij=b_it_j

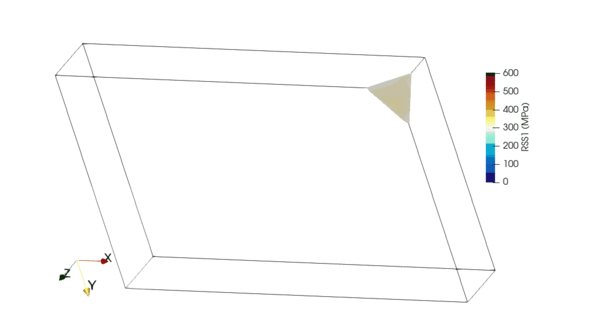
As described in the article, the Nye tensor can be related to distortions and therefore ultimately to any elastic fields (including the local Cauchy stress).

The fundamental idea behind this article is that the Nye tensor can now be determined from transmission electron microscopy observations. The ability to determine Burgers vectors from the diffraction contrast of dislocations has long been known. It is only more recently that electron tomography of dislocations has made it possible to calculate three-dimensional numerical models of line geometry, i.e. potentially, t vectors at all points.

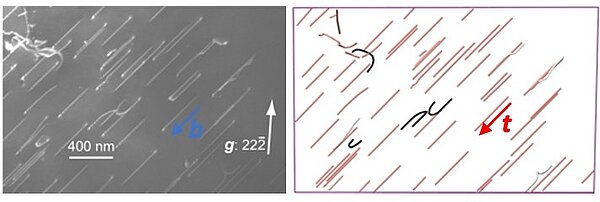
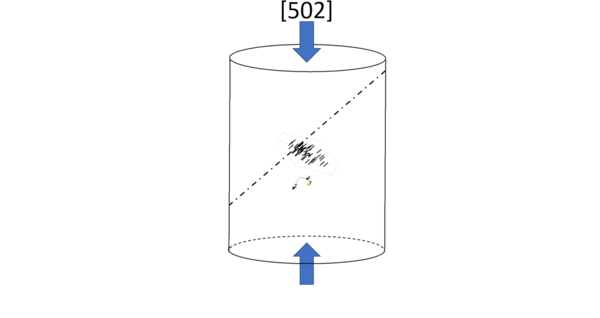
This technique is applied to a sample of olivine single crystal deformed in a previous study (Demouchy et al. 2013) along [502] in a high-resolution gas-medium high-pressure apparatus at 806 °C, with a constant strain rate of 5.1 × 10⁻⁵ s⁻¹, under a gaseous (Ar) confining pressure of 300 MPa. The thin section under study has a known orientation with respect to the applied stress